Exponential Growth And Logistic Growth

The Exponential Equation is a Standard Model Describing the Growth of a Single Population

The easiest way to capture the thought of a growing population is with a single celled organism, such as a bacterium or a cilliate. In Effigy 1, a population of Paramecium in a minor laboratory depression slide is pictured. In this population the individuals divide one time per day. So, starting with a single individual at day 0, nosotros expect, in successive days, 2, 4, 8, 16, 32, and 64 individuals in the population. We tin can see here that, on any particular day, the number of individuals in the population is simply twice what the number was the day earlier, and then the number today, call it N(today), is equal to twice the number yesterday, telephone call it N(yesterday), which we can write more compactly as Due north(today) = 2Northward(yesterday).

Since the bones rule of jail cell division applies non but to today and yesterday, just to whatsoever day at all, we would take N(6) = iiDue north(5), or N(iv) = 2North(3), etc.

So it makes sense to write this equally, Northward(t) = 2N(t - 1) where t could take on whatever value at all.

Now we can generalize this idea a chip if we note that at day half-dozen the number is equal to twice the number at mean solar day five, or North(6) = 2N(five) and at twenty-four hours five the number is equal to twice the number at solar day four, or N(5) = 2N(iv), etc.

And so in the equation for twenty-four hour period six we tin can substitute for the value of N(5) — which we know to exist 2N(4) — getting North(6) = 2[2N(4)], which is the same every bit N(6) = 22N(4).

Only N(four) = 2North(3), so we can substitute for North(iv) getting N(6) = 22N(4) = 22[2N(3)] = 23Due north(3). And if we follow the same design we see that N(three) = 23N(0), which we can substitute for N(3) to get N(6) = 26Northward(0). Thus nosotros can see a relatively simple generalization, namely

where t stands for any fourth dimension at all (e.g., if t = 6, N(half-dozen) = 26[N(0)]).

Finally nosotros note that this equation was derived from the specific situation shown in Figure 1, where one division per twenty-four hours was the hard and fast rule. That is where the two comes from in Equation 1 — from each private Paramecium we obtain two individuals the adjacent day. Of class the division charge per unit could be anything. If there were ii divisions per 24-hour interval only one jail cell e'er died, we would look three individuals from each single private and Equation 1 would be N(t) = 3tN(0). So the division rate could be any number at all and the general equation becomes,

where R is normally chosen the finite rate of population increase (in the bodily case of dividing Paramecium the finite charge per unit of population increase is equal to the division charge per unit). In Figure 2 we illustrate this equation for various values of R. It is normally referred to equally the exponential equation, and the class of the data in Figure 2 is the general grade called exponential.

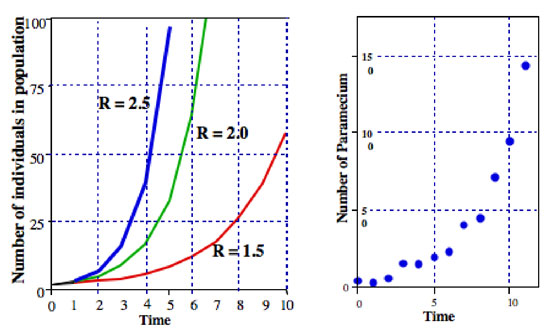
Left: general form of exponential growth of a population (equation 2). Right: actual numbers of Paramecium in a 1 cc sample of a laboratory culture.

Effigy 2: Left: full general form of exponential growth of a population (equation ii). Right: actual numbers of Paramecium in a 1 cc sample of a laboratory civilization.

Any value of R tin be represented in an infinite number of ways (e.g., if R = 16, nosotros could write R = viii x two, or R = 42, or R = 32/ii, or R = 2.718282.77). That last expression (R = 2.718282.77) makes utilise of an of import abiding that might be recalled from unproblematic calculus, Euler'due south abiding. Expressing whatever value of R as Euler's constant raised to some power is really extremely useful — it brings the full power of calculus into the picture. If we symbolize Euler'southward constant as e nosotros can write Equation 2 as

Now if nosotros take the natural log of both sides of Equation 3 — think ln(ex) = ten — Equation 3 becomes: ln [N(t)] = ln [N(0)] + rt

And if we began the population with a single individual (equally in the instance above), we have

from which we run into that the natural log of the population, at any particular fourth dimension, is some abiding, times that time. The abiding r is referred to as the intrinsic rate of natural increase (Figure 2).

All sorts of microorganisms exhibit patterns that are very shut to exponential population growth. For case, in the right hand graph of Figure 2 is a population of Paramecium growing in a laboratory civilization. The blueprint of growth is very shut to the design of the exponential equation.

Another way of writing the exponential equation is as a differential equation, that is, representing the growth of the population in its dynamic form. Rather than asking what is the size of the population at time t, we ask, what is the rate at which the population is growing at time t. The rate is symbolized as dN/dt which only means "change in N relative to alter in t," and if you remember your basic calculus, nosotros can discover the rate of growth by differentiating Equation 4, which gives us

which is kind of remarkable, considering it says that the rate of growth of the log of the number in the population is abiding. That constant rate of growth of the log of the population is the intrinsic rate of increase.

Retrieve that the rate of change of the log of a number is the same as the "per capita" alter in that number, which means we tin write Equation 5 as

where nosotros omit the variable t since it is obvious where information technology goes, and then we rearrange a bit to come up with

where the parameter r is, again, the intrinsic rate of natural increase. The bones human relationship between finite rate of increase and intrinsic charge per unit is

r = ln(R)

where ln refers to the natural logarithm. Note that Equation half dozen and Equation 3 are just dissimilar forms of the same equation (Equation 3 is the integrated class of Equation 6; Equation half-dozen is the differentiated grade of Equation 3), and both may exist referred to simply as the exponential equation.

Hypothetical case of a pest population in an agroecosystem

Figure iii: Hypothetical example of a pest population in an agroecosystem

According to model one (which has a relatively large estimate of R), the farmer needs to remember nigh applying a control procedure about half way through the flavour. According to model ii (which has a relatively small approximate of R), the farmer demand not worry about decision-making the pest at all, since its population exceeds the economic threshold only after the harvest. Clearly, it is important to know which model is correct. In this case, according to the available data (blue data points), either model i or 2 appears to provide a good fit, leaving the farmer all the same in limbo.

The exponential equation is a useful model of simple populations, at least for relatively brusk periods of time. For instance, if a laboratory technician needs to know when a bacterial civilization reaches a certain population density, the exponential equation can be used to provide a prediction as to exactly when that population size will be reached. Another instance is in the case of agronomical pests. Herbivores are always potentially major bug for plants. When the plants subjected to such outbreaks are agronomical, which is to say crops, the loss tin can be very significant for both farmer and consumer. Thus, there is always pressure level to prevent such outbreaks. Since WWII the major weapon in fighting such pest outbreaks has been chemical pesticides, such as Ddt. However, in contempo years we have come to realize that these pesticides are extremely dangerous over the long run, both for the environment and for people. Consequently there has been a movement to limit the corporeality of pesticides that are sprayed to gainsay pests. The major way this is done is to found an economic threshold, which is the population density of the potential pest below which the damage to the crop is insignificant (i.e., it is not really necessary to spray). When the pest population increases above that threshold, the farmer needs to have activity and use some sort of pesticide, or other means of controlling the pest. Given the nature of this trouble, it is sometimes of utmost importance to be able to predict when the pest will reach the economical threshold. Knowing the R for the pest species enables the farmer to predict when it will exist necessary to apply some sort of control procedure (Effigy 3).

The exponential equation is also a useful model for developing intuitive ideas about populations. The classic example is a pond with a population of lily pads. If each lily pad reproduces itself (two pads have the place of where 1 pad had been) each calendar month, and it took, say, three years for the pond to become half filled with lily pads, how much longer will it accept for the pond to be completely covered with lily pads? If y'all don't finish to think too clearly, it is tempting to say that it volition take simply equally much time, three years, for the second half of the pond to become as filled equally the first. The answer, of class, is one month.

Another popular example is the proverbial ancient Egyptian (or sometimes Farsi) mathematician who asks payment from the king in the form of grains of wheat (sometimes rice). One grain on the first square of a chess lath, two grains on the second square, and and then forth, until the last square. The Pharaoh cannot imagine that such a uncomplicated payment could amount to much, and so agrees. But he did not fully capeesh exponential growth. Since there are 64 squares on the chess board, we can use Equation 2 to make up one's mind how many grains of wheat volition exist required to pay on the last square (R raised to the 64th power, which is about xviii,446,744,074,000,000,000 — a lot of wheat indeed, certainly more in the whole kingdom). These examples emphasize the oft surprising way in which an exponential process tin atomic number 82 to very big numbers very rapidly.